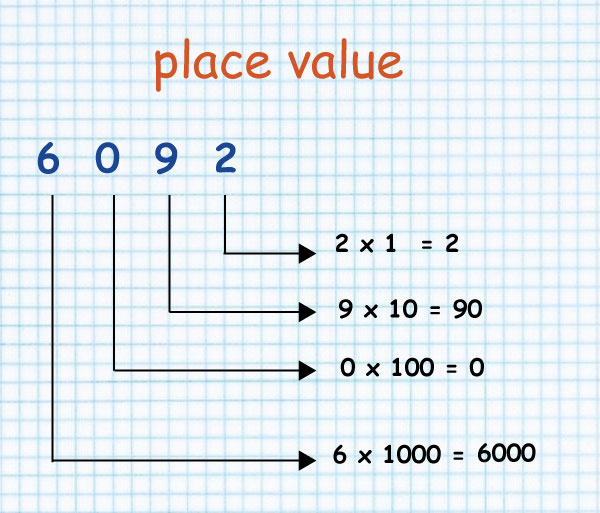
Look at the image below

- Place value and total value
- Any counting number notably: 1, 2, 3, 4, 5, 6, 7, 8 and 9 has a word that suggests its position.
- This word can be ones, tens, hundreds etc.
- These words denote the place value of a digit. Total value is the product of the digit and its place value.
Example 1
What is the place value of digit 4 in the number 58439?

Therefore, the place value of digit 4 is Hundreds.
What is the total value of digit 7 in the number 94372
Solution
| DIGIT | TOTAL VALUE |
| 9 | 90000 |
| 4 | 4000 |
| 3 | 300 |
| 7 | 70 |
| 2 | 2 |
Therefore, the total value of digit 7 is 70
The place value suggests a word while total value suggests a figure.
In maths, we use ten numbers known as symbols or digits.
From these ten digits, we can write any number.
The ten Digits we use in maths today are called "Hindu-Arabic Numerals" and look like these:
0 1 2 3 4 5 6 7 8 9
You can use these on their own to count up to 9.
http://feynman.e-limu.org/admin/curriculum/topic/290/
When you have more than 9 items, we start another column - the "tens" column -
and you write down how many "tens" you have, followed by how many ones (called "units"):
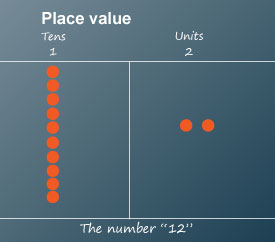
When you have more than 99 items, you start another column - the "hundreds" column.
Now you need to show how many hundreds, tens and units:

So you know that you have 1 Hundred, 4 Tens and 3 Ones
This could also be written as 1 × 100 + 4 × 10 + 3 × 1.
When you write numbers, the position (or "place") of each digit is important.
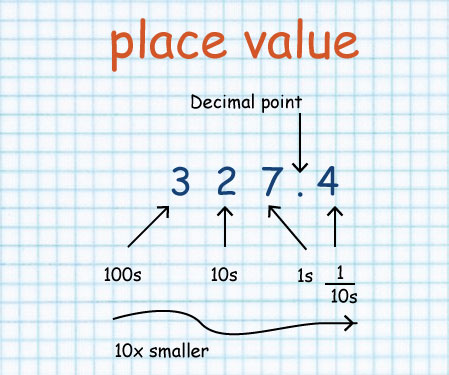
In the number 327:
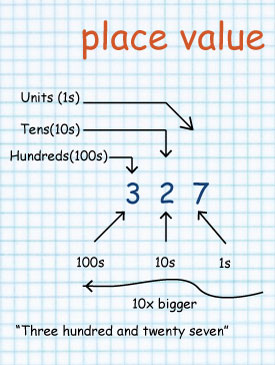
| As you move left, each position is 10 times bigger! | |
| Example: Hundreds are 10 times bigger than Tens |
... and ...
| As you move right, each position is 10 times smaller. | |
| From Hundreds, to Tens, to Units |
But what if you continue past Units?
What is 10 times smaller than Units?
1/10 ths (Tenths) are!
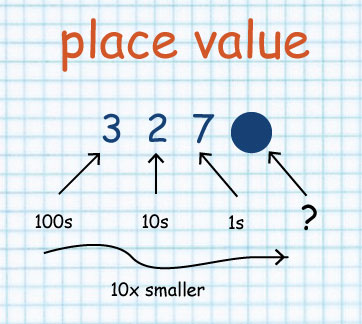
But you must first write a decimal point,
so you know exactly where the Units position is:
You can continue with smaller and smaller values, from tenths, to hundredths, and so on, like in this example:
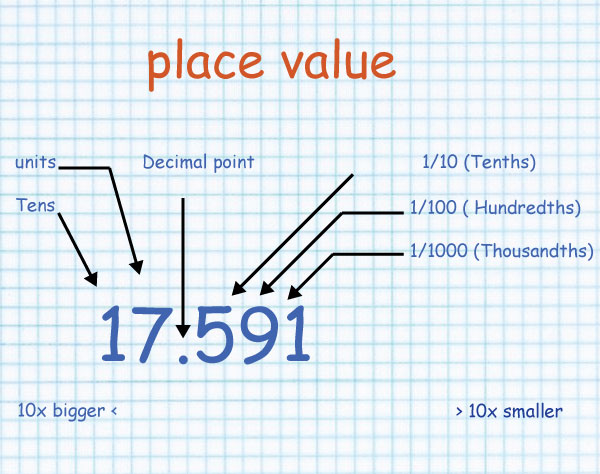
The face value of a digit is the digit itself, at whatever place it may be.
It is unchangeable and definite.
But place value changes according to the digit’s place.
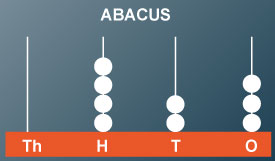
This abacus shows the number 423.
According to the abacus,
4 beads are at H-place (hundred-place)
2 beads are at T-place (ten’s place)
3 beads are at one’s place
Hence, the number = 400 + 20 + 3 = 423
Now, having the knowledge of face value and place value of the digit, we ascertain the total value of a number; as:
In 423;
the face value of 4 is 4 and place value of 4 is 400
the face value of 2 is 2 and place value of 2 is 20
the face value of 3 is 3 and place value of 3 is 3
So, 423 = 400 + 20 + 3
It is read as, four hundred, twenty and three or four hundred twenty three.
|
3 is 3 × 1000 = 3000 7 is 7 × 100 = 700 2 is 2 × 10 = 20 0 is 0 × 1 = 0 |
3 being at Th-place 7 being at H-place 2 being at T-place 0 being at one’s or unit’s place |
Place value of the digits 3702 are shown below:
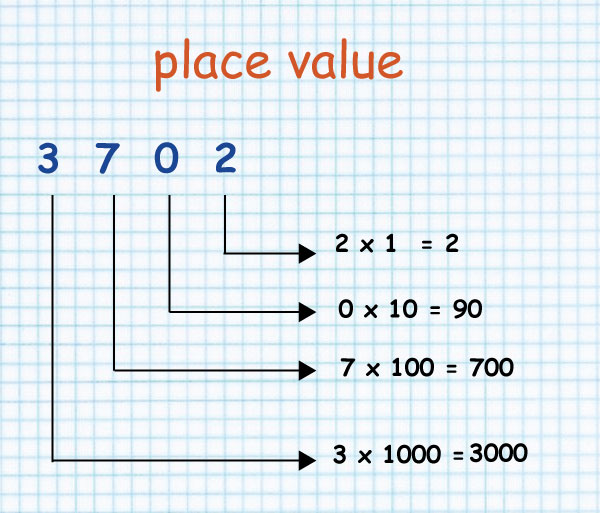
The place value of the digit 0 in a number is always zero, whatever may be its position.