The letters GCD stands for Greatest Common Divisor
The letters HCF stands for Highest Common Factor
Note: GCD is also called as HCF.
Lets break the words further down and ask ourselves.
What is a Factor?
Factors are the numbers you multiply together to get another number
For example:
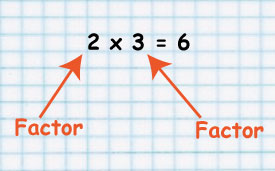
Examples of numbers and their factors are:
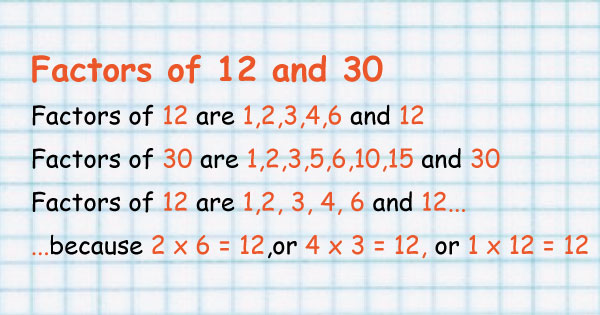
So, what is a "Common Factor" ?
Let us say you have worked out the factors of two numbers:
Factors of 12 are 1, 2, 3, 4, 6 and 12
Factors of 30 are 1, 2, 3, 5, 6, 10, 15 and 30
It is a common factor when it is a factor of two or more numbers.
(It is then "common to" those numbers.)
Look at this example:

It is simply the largest of the common factors.
In our previous example, the largest of the common factors is 15, so the Greatest Common Factor of 15, 30 and 105 is 15
The "Greatest Common Factor" is the largest of the common factors (of two or more numbers).
Look at this example:
Find the Greatest Common Factor of 12 and 16

The following are the methods of finding greatest common divisor.
To find the GCD of 4, 8 and 16 using Method 1: listing method, we proceed as follows.
Divisors or factors of 4 are 1, 2, and 4
Divisor or factor of 8 are 1, 2, 4 and 8
Divisors or factors of 16 are 1, 2, 4, 8 and 16.
Note: To remember these factors, think of the families of 4 or which numbers to multiply to give 4.
Note: 1, 2 and 4 are common factors of 4, 8 and 16.
The highest or greatest of these is 4.
Therefore, the GCD or HCF of 4, 8 and 16 is 4.

To find the GCD of 4, 8 and 16 using
Method 2 :
Prime factorization we proceed as follows.
1. Draw up lines as shown on the table below.
2. Start with the smallest prime number that can divide all numbers without a remainder.
3. Proceed until all prime numbers that can divide the numbers are applied.
4. Multiply out the prime numbers on the left hand side.
The GCD of 4, 8 and 16 is 2 X 2 = 4
Method III: Power method
To find the GCD of 4, 8 and 16 using power method we proceed as follows.
Step I: Write the numbers as a product of their powers.
Step II: Pick the numbers involved with the lowest power and should be common.
Step III: Multiply out.
4 = 2 X 2
= 22
8 = 2 X 2 X 2
= 23
16 = 2 X 2 X 2 X 2
= 24
The GCD of 4, 8, 16 is 22
= 2 X 2
= 4
Note:
All sets of numbers can have LCM but not all sets have GCD.
Play this video and learn more on how to find GCD of numbers
GCD is useful when we want to simplify a fraction.
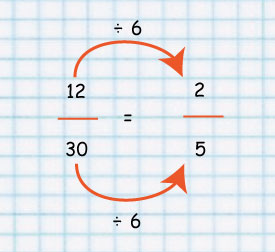
How could we simplify 12/30 ?
Common Factors of 12 and 30 are 1, 2, 3 and 6, and so the Greatest Common Factor is 6.
So the largest number we can divide both 12 and 30 evenly by is 6, like this: