Algebraic expression is a meaningful combination of numbers and letters.

Difference between an algebraic equation and an algebraic expression.
An algebraic equation has an equal sign while an algebraic expression does not have an equal sign.


Note:
An algebraic expression cannot be simplified any further.
Steps followed in forming algebraic expressions are:
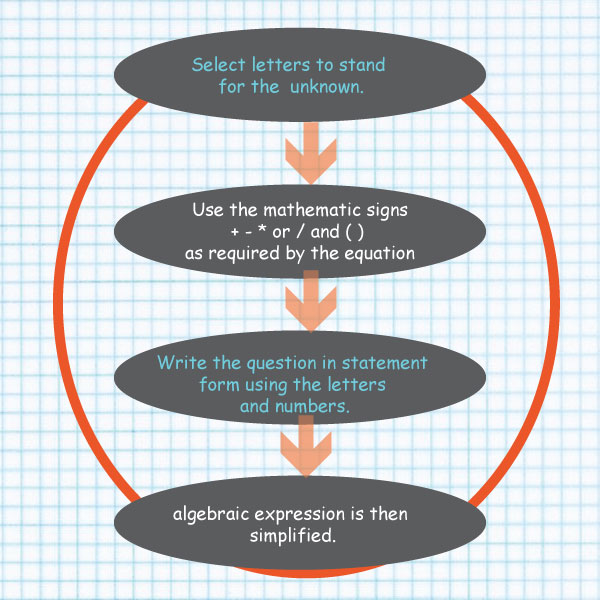
Wanja’s age is four times the age of Atieno.
Calculate the sum of their ages in five years time.
Let the age of the younger person (Atieno) be x
Therefore Wanja’s age is 4x
After 5 years:
Wanja’s age will be 4x + 5
Atieno’s age will be x + 5
Sum of their ages = x + 5 + 4x + 5
Collect the like terms: x + 4x + 5 + 5
= 5x + 10 years
= 5(x + 2) years
A group of pupils went for a trip in x vehicles.
If y vehicles carried 20 pupils each, find the number of pupils who went for the trip if the remaining vehicles carried 15 pupils each.
Number of vehicles = x
Total number of pupils carried by y vehicles
= 20 multiplied by y
= 20y pupils
Remaining vehicles
= (x – y)
Total number of pupils carried by the remaining vehicles
= 15 multiplied by (x – y)
= 15(x – y)
Open the brackets
15x – 15y pupils
Total number of pupils who went for the trip
= 20y + 15x – 15y
collect the like terms together
= 20 y( – 15y ) + 15x
= 5y + 15x
= 15x + 5y
The length of a rectangle is thrice the width. If the perimeter is 48cm, what is the width?
Look at this,

Lets have x to represent both the length and the width.
Relate length to width ,so let y stand for width and 3y for length. see the image below.

Perimeter = length + width + length + width
=2(l+w)
Substitute length with 3y
And width with y
48cm = 3y + y + 3y + y
48cm = 8y (divide both sides by 8)
y=6cm
Therefore the width of the rectangle = 6cm
And the length = 3(6)= 18cm
Example 4

Solution
Let the number be k
Multiply it by 3 to get 3k
Add 6 to the product = 3k+6
The result is 21, so the equation is:
3k + 6 = 21
Solve the equation by
Subtracting 6 from both sides of the equation
3k+6-6=21-6
3k=21-6
3k = 15 (dividing both sides by 3)
K/3=15/3
Therefore:
K=5
The Number is 5